Vibration and Distance

Search Vibrationdamage.com

Most people understand that, the farther you are away from an event, the less likely you are to be affected by it. Indeed, distance from the source of a vibration is probably the single most important factor, after the amount of energy that goes into creating the vibration (i.e. the "source energy"), in determining both whether it will have damaging effects on a home or structure and how disturbing people will perceive it.

Here, I'll provide an introduction to the complex matter of how vibration velocities (intensities) decrease with distance. I will discuss some of the basic factors which affect vibration movement through the ground, how vibration velocities (peak particle velocities, PPV's) can be mathematically calculated (as plotted at left) and the significant cautions that one must observe in using those estimates. This chapter of the CVDG is heavily footnoted with scientific references and additional detail, which those with more than a passing interest will want to read.

About the PPV/Distance Diagrams

There are several diagrams of calculated vibration velocities and safe distances in this chapter of the CVDG, like those at right and above. Calculated ground vibration velocities can be read off any of the diagrams for any distance from 5 to 250 feet from the vibration source just by noting where the distance to the construction work (source)^[15] intersects the appropriate curve, then reading the velocity at that intersection from the vertical scale.  You can view, in a new tab or window (and print a copy from your web browser for personal use, if you wish), a full-size version of the distance-ground vibration velocity and safe distance relationships which follow just by clicking on each diagram.^[8]  Registered CVDG for Homeowners and CVDG Pro purchasers can also download a complete free PDF collection of full-sized versions of all the vibration velocity diagrams in this chapter of the CVDG.

How Far Away Is "Far Enough"?

Although questions like this are often asked and conclusions given, there is no single answer to the question, "How far away must my building be from a vibration source to be considered 'safe' from vibration damage[?]". Buildings have different degrees of resistance to vibration damage depending on design, construction materials and age, among other factors.^[28] As discussed below, both vibration source properties (e.g. pile driving vs. compaction) and the way vibration velocity decays through movement in the ground can be very different, depending on locale, presence or absence of structures and other obstructions which can damp, reflect, refract or modify vibration waves. Resonance effects in homes and other buildings can turn an "allowable" ground vibration into a structure vibration which is damaging at considerably greater distance than the direct ground vibration itself might be. Even the specific way in which an operator carries out a certain construction operation (e.g. compaction) can have a very large impact on the vibrations created.

Commonly-asserted statements like, "You are too far away from the work to have damage", have meaning, at most, only in the limited sense of relative probability of damage (see Vibration and Damage), even in the comparatively rare examples in which they are correctly founded upon real scientific insight. Given the many uncertainties which surround vibration damage probability for a given situation and structure, the best, safest, and, in the end, the cheapest approach is usually the one which minimizes the probability of damage in every reasonable way possible.

Spreading and Decrease of Vibration Energy

As discussed generally in the CVDG's Vibration 101 chapter, vibration peak particle velocities, PPV's, decrease as distance from the source increases. Stated more scientifically, the vibration velocities depend "inversely" on distance. The inverse dependence is, at root, mostly a geometric effect. For body waves, the vibration velocity decreases as a given amount of source vibration energy spreads out over a sphere, whose area increases as the radius squared. Although the geometry can explain a good deal of the decrease of vibrations with distance, soil compositions, including the amount of water they carry, also affect the vibration intensity through their different degrees of damping.

Ground vibration intensities are usually measured by seismographs, like that shown at left. Unfortunately, vibration monitoring of this sort is only rarely performed during construction projects, even when such monitoring is a contractual obligation (as in most Federally-funded road construction). Calculations often become the only way to estimate vibration velocities in a given construction operation or damage possibly stemming from it.

Variations in Created Vibrations and Their Transmission

The specific way that the vibration velocity varies with distance is affected by many variables. Some of these pertain to the factors which govern the vibration velocity created at the source, while others relate to the way in which vibrations propagate (move) from the source and attenuate (become lessened) in the ground. A partial list of these effects follows:

Source Vibration Energy Effects

• differences in vibrations created by different types of equipment (e.g. pile drivers vs. compactors),
• significantly different vibration characteristics of different versions of the same equipment (e.g. vibratory vs. oscillatory compactors, hammer vs. vibratory pile drivers),
• operator-variable settings (e.g. vibration amplitude for vibratory compactors) on a given model and type of equipment,
• operator variations in the way the equipment is used, even on the same day at the same location
• run-to-run changes to the source energy (e.g. from different blasting charge weights, short duration vibration spikes at heavy equipment start and stop, variable compaction vibration amplitudes, variable transmission of vibration to the soil, size and type of pile driver, and many others)
• predominant direction of source vibration (to/from vs. up/down vs. side/side),
• frequency distribution of the vibration components as a function of the source and its mode of operation

Soil Vibration Transmission and Attenuation Effects

• frequency distribution dependence on distance,
• the specific vibration path through the soil (e.g. whether on the surface or at depth),
• specific pattern of soil particle movement (e.g. Love waves vs. Rayleigh waves) with respect to the vibration propagation direction,
• vibration vector (e.g. longitudinal vs. vertical),
• soil type and composition,
• soil compaction,
• soil moisture,
• soil stratification (i.e. layering),
• embedded soil obstacles (e.g. sub-surface boulders in glacial till and mountain soils)
• underlying geology,
• extent of natural rock fracturing,
• wave interference and reflection effects,
• localized vibration wave focusing, due to soil refraction effects,
• localized soil layer resonance with vibration waves,
• presence of structures,
• landscaping features

Not all these factors will play a significant role in affecting the vibration velocity in every setting, though, typically, a majority of them are likely to be relevant in most construction vibration situations.

Limitations in Calculating Vibration Velocities

Many of these features can be included in calculations of vibration velocities, at least in principle, if enough information is known about the vibration source, locale soil type and underlying geology. Such detailed information about both the vibration source and the vibration attenuation environment is, at best, only rarely available in real life construction vibration examples. Other factors are so site-specific and require so much information (e.g. embedded objects, reflection and interference effects, presence of buildings, landscaping) that they are virtually impossible to take into account fully in the general-use equations commonly employed for predicting vibration velocities. Note that none of the cited factors take into account directly variations in building resistance to vibration damage, which is a separate issue discussed in the CVDG chapter, Vibration and Damage.

The many variables which affect vibration transmission can make accurate calculations of vibration velocities challenging, in the absence of substantial validation of the calculation results by comparison with measurements made literally on the site of interest. However, calculating (and measuring) how vibration velocity changes with distance is central to an ability to estimate "safe distances" (check the CVDG Pro's Vibration Safety chapter for more on such estimates) from construction work or to use vibration propagation equations meaningfully in any other way. Thus, such calculations are widely used, even if, all too often, with limited accuracy, improper interpretation and over-reliance on the specific numerical result.

Simple Estimates of Vibration Velocities

One of the most commonly used relationships for estimating construction-related vibration velocities is that offered in the U.S. Federal Transit Administration's Noise and Vibration Manual:^[1]

PPV_equip = PPV_ref  x  (25/D)^1.5

where: PPV_equip is the calculated peak particle velocity in units of in/sec of the construction equipment type at the distance of interest, PPV_ref is the reference vibration level for that type of construction heavy equipment in in/sec at the reference distance of 25 feet, from Table 12-2 of the FTA Noise and Vibration Manual,^[1] and D is the distance from the equipment to the structure or seismograph, in feet. This equation combines all the physical details of vibration movement ("propagation" or "attenuation") through the ground in the 1.5 exponent and all the characteristics of the source vibration in the reference velocity, PPV_ref, which is a reflection of the source energy and how efficiently that energy is transmitted to the ground.^[36] In this equation, the distance from the vibration source, D, is in the denominator of the fractional rightmost factor. So, the calculated vibration PPV decreases as the distance increases, just as you would expect.

The FTA equation is phenomenological - it is fitted to vibration data, using measured reference values for equipment vibration, rather than taking into account directly in its factors most or all of the known physical variables which affect vibration propagation. Thus, there is limited direct relationship between its parameters and fundamental quantities affecting vibration transmission which one can relate back to physical laws, source energies and soil properties. It is a considerably simplified, but often useful, approach to describing some aspects of construction vibration transmission through the ground, and, then, to buildings.

Using the FTA Equation

Immediately below is plot of calculated ground vibration velocities for vibratory compactors, according to the FTA equation. In this semilog plot, the velocities are plotted on the vertical scale with equal distances between equal values (i.e. linear), while the distance scale is logarithmic,^[7] with powers of ten (1, 10, 100, 1000, etc.) of the distance having equal separations. Such logarithmic plots enable one to see better the relationships when large spans of numbers are to be shown. That fact can be easily seen by comparing this plot with the small all-linear version at the start of this chapter.

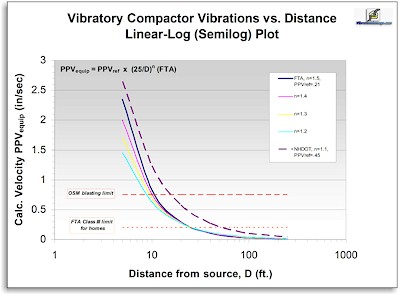The velocities calculated in the diagram above are for various values of the FTA equation exponent, as might be needed for soils of differing type, using a vibratory compactor with an FTA reference velocity, PPV_ref, of 0.210 in/sec. Also shown are values calculated from more recent, revised values of the exponent and PPV_ref from a U.S. state of New Hampshire Department of Transportation (NHDOT) study.^[2],[3]

This diagram illustrates that the value one calculates for a vibration velocity at a specific distance is determined by the choices of PPV_ref and the exponent that one makes. If values for these parameters are chosen which do not reflect or properly account for the actual source vibration characteristics, the local soil and geology conditions, or other factors not explicitly included in the equation (e.g. wave reflection and interference), the calculated values will differ, sometimes substantially, both from values calculated using other numbers for PPV_ref and the exponent - and from measured vibration velocities.

Vibration Velocity Calculations and Standard Limits

The OSM blasting standard limit for vibration mid-frequencies in undamaged homes of modern construction, without plastered walls, and the FTA Class III limit for timber-framed homes are also shown as horizontal lines in the diagram. "Acceptable" vibration peak particle velocities for each of those two standards lie below the lines shown. Velocities exceeding those standards lie above the dotted horizontal lines. Any vibration velocity above these standards has a higher, and rapidly increasing, probability of causing damage than one falling below the standard, at least in the circumstances for which the standards are intended (see the CVDG chapter Vibration Standards for more about ground vibration standards and their use and Vibration and Damage for more on damage probabilities).

The OSM standard is only applicable to examples where the vibration source is blasting, either in mining or, with less assurance, in construction. Construction heavy equipment-caused vibration should be governed by the one of the FTA limits in the U.S., of which the Class III limit for timber-framed homes (most homes in the U.S.) is shown in the diagrams in this chapter. The related Swiss machines and traffic standard is also relevant for construction ground vibration and more confining than the FTA standard (see Vibration Standards for more detailed information) in several ways.

None of the curves in this chapter show predicted home or building vibration velocities. The structure velocities are both structure type and position-dependent. They may be substantially higher (see Resonance/Fatigue for more on this) than the ground velocity, due to varying degrees of resonant amplification of the ground vibration in the structure.^[27]

Another Depiction

In the next diagram below, the same calculations are represented on a "log-log" plot, in which both the calculated velocity on the vertical scale and the distance on the horizontal scale are logarithmic. This depiction is the way that such vibration velocity/distance relationships are usually shown in the scientific literature. It allows a wide range of values to be shown on both the vertical and horizontal axes. Plotting the calculations in this way has the effect of turning the exponential curves into lines with a slope, -n, of the FTA equation exponent.^[7]

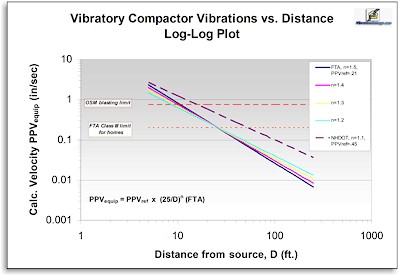As the diagram shows, there are significant differences in the calculated velocities as one changes the value of the exponent in the FTA equation. The less negative the value of the exponent, the slower the vibration velocities decay with distance and the farther high PPV vibrations can move before their ground PPV's fall below standard limits. Indeed, the NHDOT studies, based on newer data for more modern road construction equipment,^[2] found significant deviations from the FTA suggested values of 1.5 for the exponent, n, and the FTA suggested PPV_ref value of 0.210 in/sec for vibratory compactor use at 25 feet. NHDOT found that its own data were fit better by an exponent of 1.1 and a PPV_ref for vibratory compactors of 0.45 in/sec, as shown in the diagram above.^{[3],[16],[36]}

Both these changes have the effect of making the "safe distance" for such compactors considerably larger than the FTA equation calculation indicates, as seen in the plots in this chapter. The more up-to-date NHDOT data have the effect of doubling one estimation of "safe distance" (i.e. that distance at which the calculated vibration velocity drops below the FTA Class III standard for timber-framed homes) for vibratory compaction (as seen at left) from about 30 feet to over 60 feet. Note that the compactor in the photo is being used considerably closer to homes than 60 feet.^[4],[24] Extensive damage to many homes was done during the road reconstruction project shown in the photo.

Neither the FTA nor the New Hampshire vibration attenuation equation parameters are necessarily appropriate for all locales. Indeed, there are some areas where vibration attenuation is much less rapid than in the studies on which the parameters are based. For example, a study for the U.S. state of Florida DOT, with 170 data points involving vibratory and static compactor use over various compaction bases throughout Florida, shows an exponent, n, of -0.6, indicating a much slower decrease in the PPV as distance increases than in either the New Hampshire or original FTA reports. The range of PPV's at or near 25 feet (the FTA reference distance) for the compaction work in Florida covers a range from 0.05 in/sec to 0.5 in/sec, depending on compacted material, with most measurements near the upper end of the range.^[20]

Just below is a comparison of calculated vibration velocities for vibratory compactors, using the FTA, FLDOT and NHDOT parameters in the FTA equation. The diagram shows that a calculated "safe distance" (i.e. that distance at which the vibration velocity falls below the FTA Class III limit) ranges from around 25 feet for the FTA parameters, to nearly 60 feet for the NHDOT parameters, to 100 feet for those calculated from the extensive FLDOT study results.^[21],[24]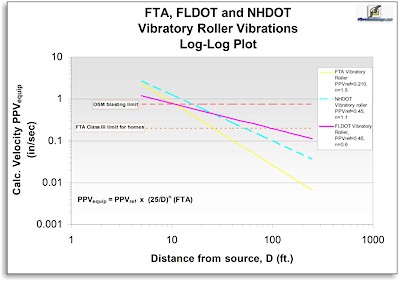

We consider the New Hampshire data to be instructive, representative and reasonably conservative with respect to vibrations in most, but not all, other locations. When there is predictable potential for damage to the property of uninvolved third parties, as is almost always the case in construction damage incidence, the conservative approach is the one which should be followed. Therefore, the New Hampshire values for PPV_ref and the exponent of 1.1 in the FTA equation are currently the recommended ones to use,^[6],[36] in the absence of specific and detailed vibration propagation data (e.g. like those from Florida), pertaining directly to the location of interest, which indicate use of even more conservative parameters.

Other, modified versions of the FTA equation have been proposed and utilized for specific equipment types (e.g. pile drivers) and situations. In most of these examples, the value of the exponent n suggested is 1.1,^[6] in accord with the NHDOT study. The lower value of n results in a slower reduction of the vibration intensity with increasing distance than the FTA equation standard exponent value of 1.5 would indicate. The NHDOT and FLDOT studies, among others,^[6] demonstrate that neither the 1.5 exponent nor the reference equipment ground vibration velocities given in the FTA vibration manual are current or appropriate in all circumstances.^[2],[6]

Other Equipment Types

While vibratory compaction is the most common apparent damage cause reported to Vibrationdamage.com, it is not the only type of construction operation with damage potential. Following is a comparison between FTA equation velocities calculated with parameters for both compactors and pile drivers, another class of equipment with significant damage potential.

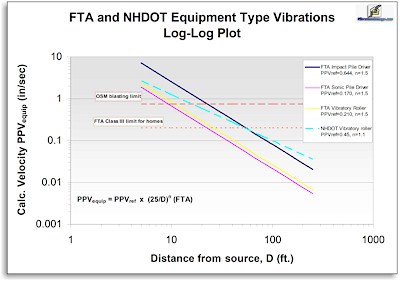As the diagram shows, both pile drivers and vibratory compactors can produce ground vibrations whose velocities exceed the FTA Class III limit for timber-framed homes and, close in, even the OSM mid-frequency blasting limit.

The NHDOT study also provides updated PPV_ref values for a broader variety of different equipment types and operations, along with the suggested value for the exponent of 1.1, for use in the FTA equation. Just below is a log-log plot of calculations with the NHDOT PPV_ref values for a wider range of construction equipment.^[22]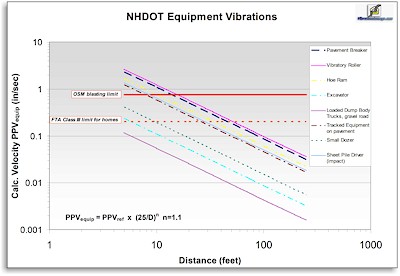

The plot shows that some operations, particularly vibratory compaction, pile driving, use of hoe rams (hydraulic rock breakers mounted on excavators) and driving tracked vehicles over distance, can be expected to exceed one or both standard limits over at least some distance ranges. Particular attention must be paid to all types of construction operations to make certain that they are not carried out within those distance ranges and/or are appropriately mitigated to reduce damage probabilities (see Vibration 101 and Avoiding Vibration Damage in the CVDG and Vibration Mitigation in the CVDG Pro for details).

Another class of operations which has significant damage potential, ground impacts, is not included in the diagram, because they can be done in so many different ways and create widely variable vibration velocities, only some of which are likely to cause damage. Demolition is one example of ground impact which can be particularly concerning, even though its vibration velocities are difficult to estimate in advance or in any given project. Other operations, like crack-and-seat procedures, dumping rocks or broken concrete, and dynamic compaction, can also produce ground impacts which may be of concern.

The calculations in these diagrams are only extended to 250 feet from the source, as the diagrams demonstrate that most forms of heavy equipment-related vibration velocities will be below the FTA Class III limit for homes at that distance in most locales with "normal" vibration attenuation, even when a factor of two "safety factor" is included. Conditions of low vibration attenuation (e.g. localities in Florida), interference effects in the ground vibration, or vibration frequency-related resonance effects in the home may act to make specific examples of equipment use, and especially blasting, dangerous for homes at distances well beyond 250 feet in some circumstances.^[25],[27]

Source Energy Effects

Many types of construction heavy equipment, in different models, can be used in different ways by operators which can substantially affect the ground vibration velocities they produce. For example, pile drivers can be divided into different "energy classes" which reflect the amount of vibration energy transferred to the ground and the ground vibration they produce. Hammer pile drivers generate more vibration at the source than resonance (or vibratory) pile drivers. Heavy truck and equipment traffic vibration depends on the weight and speed of the vehicle and the road condition. The CVDG Pro chapter, Calculating Vibration Amplitudes, has much more information on source energy effects on vibration velocities. By way of illustration, we'll take one of the most common causes of vibration damage, vibratory compaction, and briefly explore here some of the factors which can influence how much compaction energy is transferred into ground vibrations.

Vibratory compactors (like the examples shown at left and above)^[19] and rollers are the single most reported suspected cause of damage to homes at Vibrationdamage.com. They present special problems in prediction of their produced ground vibrations and, thereby, their damage potential.^[38] Different compactor models have different drum weights and widths, different and often operator-variable centrifugal force limits for the drum vibrations, operator-variable compaction amplitudes, different rates of travel, different types of vibration motions (cf. up-down vibratory vs. back-forth oscillatory compactors^[11],[26] vs. vibratory-oscillatory compactors employing both types of motion) and different, sometimes operator-modifiable, vibration frequencies.^[16],[19] All of these factors are known to affect the velocity and frequency distribution of the ground vibrations produced when compactors are used in non-static modes.^[23] Yet, full knowledge of the state of all of them is almost never available in real-life compaction damage situations.

Compactors using lower frequency (generally under 40 Hz) vibrations create vibrations in the ground which have greater range (and larger safe distances) than those compactors whose nominal vibration frequencies are higher, due to more rapid attenuation (loss) of the higher frequency vibrations in the ground with distance.^[17] Low frequency vibrations also transfer vibration more efficiently to home resonant motions than higher frequency ones. The same compactor, operating with the same setup and operator, may display different dominant frequencies, depending on distance from it, as a result of wave interference effects between the vibrations from the two drums (see Vibration and Damage for an example and Vibration Signatures in the CVDG Pro for more on this issue).

Similarly, at startup and stop,^[37] or if vibration is not turned off when the compactor reverses direction, as is often the case in construction work,^[18] relatively short duration ("transient") vibrations, of considerably higher velocity than the normal, "steady-state" ones, can be produced at each reversal as a result of "pile-up" of vibrations.^[11],[18] The degree of compaction also affects the vibrations generated; initial passes of the compactor generate less ground vibration than subsequent ones, as the degree of compaction increases.^[39] Even the direction of compaction (forward vs. reverse) can influence the vibrations created.^[40] The effect of the many variables which affect compactor vibrations, whose specific contributions are usually unknown in a given situation, can mean that calculated ground velocity values for compactors, even when reasonably close to some measured average values, may not correctly reflect true damage potential in all uses of the compactor, even for the same compactor models on the same job.^{[19],[35],[41]}  The CVDG chapter, Avoiding Vibration Damage, provides a longer description of ways to mitigate vibration in a wide range of construction operations.

Using Vibration Calculations

As indicated earlier, it is relatively rare for vibration monitoring to be done on construction jobs (as shown in the image at right of a seismograph transducer head in use during a construction road repair), even though many public construction contracts require vibration monitoring as part of their "boilerplate" contractual conditions. Thus, the typical homeowner facing construction vibration, and possible damage from it, will have no or limited access to measurements of vibration velocities to compare with the diagrams on this page.

This is one of the reasons that we have recommended that homeowners do some monitoring of their own (see our Vibration Monitoring chapter for much more on vibration monitoring, both "professional" and "do-it-yourself") to get an idea if felt vibrations actually have damage potential. However, in the absence of actual data, it is important for homeowners to know which operations have significant damage potential and which ones are of lower risk. Such information will help them in making knowledgeable judgments about felt vibrations and in understanding the real meaning of vibration data, when the data are available or when conclusions from monitoring or calculations are offered to homeowners.

Indeed, even the more recent NHDOT data underestimate vibration velocities at distance in some areas (e.g. many parts of the U.S. state of Florida^[9],[12]) which have especially low vibration attenuation, as indicated above). Correlations exist between soil type and the value of the equation exponent, n. Softer soils attenuate vibration more efficiently (producing typical exponents up to 1.6); a 1.0 exponent is suggested for hard rock.^[6] Some locales will show values of n outside the 1.0-1.6 range (e.g. 0.6 for vibratory compaction in the Florida data). Even in relatively homogeneous and well-characterized soils, random variations in soil composition can affect vibration velocities in largely unpredictable ways.^[43]

Although Vibrationdamage.com and its Facebook page emphasize effects of vibration from construction heavy equipment, blasting is sometimes done in construction contexts to remove rock or level sites on rock. Construction blasting differs substantially from mine and quarry blasting in the typical amounts of explosive used per delay and the frequency distribution of the produced vibration.^[29] Of course, it differs from heavy equipment vibration production, too, even though it is another energy source driving vibration, broadly similar to the driving energy provided by heavy equipment use.

Blasting vibration-distance relationships are usually depicted differently in scientific contexts than other kinds of construction vibration. The diagram below, depicting actual blasting vibration data from a construction project involving leveling and terracing of a planned housing development area on a volcanic rock site,^[32] shows how blasting vibration velocities are typically plotted vs. a quantity called "scaled distance",^[9] rather than measured absolute distance. The scaled distance, usually denoted in the relevant literature as SD or D_s, is just the measured distance between the blast and the seismograph recording the vibrations, divided by the square root of the charge weight of explosive used per explosion delay.^[30],[31]  Charge weights per delay (usually around 8-9 milliseconds between the multiple closely-timed detonations which comprise one blasting "shot") are nearly always reported in documents to local regulatory authorities in "blasting logs", as required by local and state blasting regulations. When seismograph monitoring is required by regulation, the measured vibrations at the seismograph locations and their absolute distances from the blast site may also be disclosed to authorities. 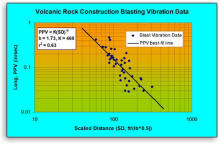To determine whether monitoring is required by law, the blaster must calculate the scaled distance value from the distance to the nearest structure and the charge weight to be used in the blast.

When plotted with logarithmic scales on both axes, as shown in the diagram at left, the equation describing the vibration intensity as a function of scaled distance, PPV = K(SD)^-b, (often generally referred to in the scientific literature as "power law scaling") produces a line, whose slope is generally related to the type of soil or rock through which the vibration moves. Very soft soils or soft rock produce values of b up to about 1.8, with a typical value of 1.6; harder soils or rock produce values of b as low as 1.0.^[42] This kind of exponential equation transformation to lines on a log-log plot is directly analogous to that seen in log-log plots of heavy equipment vibration attenuation shown earlier in this chapter.

Other information about blasting vibration science is found throughout the CVDG, including an introduction to blasting and its effects in the CVDG chapter, Blasting Vibrations. The CVDG Pro chapter, Calculating Vibration Amplitudes, has considerably more information about blasting vibration and means of modeling its decrease with distance.

"Safe Distances"

As indicated earlier, a calculated distance at which a vibration velocity falls below a properly chosen standard limit can be suggestive of a "safe distance", at least for those types of activities for which the standard is intended and defined. Properly determined and applied safe distances have value because they are easily implemented. They can provide quick insight into which operations might be considered inherently unsafe with respect to damage potential, if they are expected to be done inside the calculated safe distance. Safe distances represent guidelines; an operation carried out at less than the safe distance has a higher probability of causing damage than one done at a distance greater than the safe distance for that operation. Given the sigmoidal shape of the damage probability-velocity curves (see Vibration and Damage), the damage probability increases rapidly, the further inside the safe distance one encroaches, or, put another way, the more one exceeds the ground vibration standard PPV limit.

The FTA attenuation equation, and modifications of it, can be used to approximate "safe distances" for construction operations, as illustrated in the diagrams above and at left. Minimum safe distances can be derived by calculating directly using a version of the FTA equation^[33] (or reading off the diagrams above) the distance at which the PPV drops below the standard. Because safe distances determined in this way are subject to the inherent errors and limitations of the velocity calculations, as well as the statistical uncertainties underlying the standards on which they are based, they are best considered as minimum safe distances. For this reason and others, prudence requires that calculation-based safe distances always have at least a factor of two safety margin applied to them, as discussed further below.

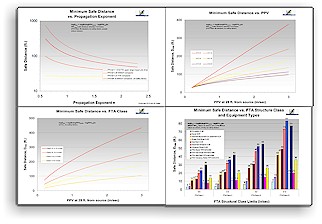
The graphic below shows some minimum safe distances in feet (without safety factors) calculated in this way for various pieces of construction equipment, using the FTA propagation equation with the more up-to-date equipment reference PPV's and 1.1 propagation exponent from the NHDOT.^[24]

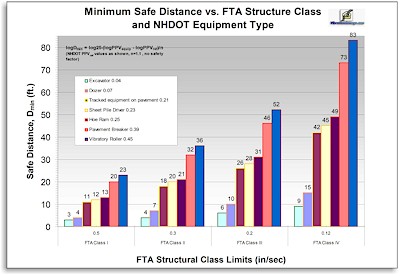
The safe distance values indicated may be conservative (i.e. "too far") in some locations having soils and geology exhibiting more negative propagation exponents than the NHDOT suggested value of 1.1 and overly optimistic (i.e. "too close") in other locations, like much of Florida in the U.S., with lesser attenuation exponents. The effect of the attenuation exponent, n in the FTA equation, on the calculated safe distance (using the FTA Class III standard velocity limit of 0.2 in/sec) is shown in the graphic at right for several different heavy equipment types.^[33] 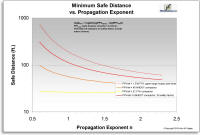As can be seen in the diagram, the higher the value of n, the faster the vibration dissipates and the lesser the calculated "safe distance". This variable is discussed more fully in the CVDG Pro's Calculating Vibration Amplitudes chapter. There are even variations within types of operations done with different models of the same general equipment type.^[11]

There will be some circumstances in which construction operations must be performed inside safe distances to which safety factors have been applied. In those examples, simple mitigation steps must be taken to limit vibration and vibration monitoring carried out to assure the success of mitigation. More technical information on the meaning, applicability of, and cautions involved in using vibration safe distance calculations, with additional safe distance diagrams, can be found in the CVDG Pro's Vibration Safety chapter.

Registered CVDG and CVDG Pro users also gain free access to our Ground Vibration PPV and Safe Distance Calculator, which allows them to do calculations, specific to their own situations, rapidly and simply. 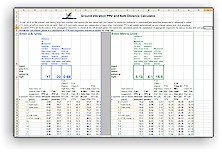The diagrams and Calculator (one part of which seen at left) can be used to verify claims made by construction companies regarding expected vibration velocities, estimate vibration velocities, when no monitoring data are available, approximate safe distances for a variety of construction operations and local soil and geological conditions and identify potentially damaging construction operations which are close enough to structures to require vibration mitigation steps. The Calculator also has a blasting vibration calculator which uses the scaled distance approach and a blasting damage probability calculator.

Proper Use of Vibration Calculations

Sometimes, vibration propagation equations are used inappropriately and without benefit of current scientific understanding of the appropriate exponent and PPV_ref for a given construction location and operation. Such uncritical application of the equations can lead to even larger errors in calculated safe distances with respect to measured velocities than those inherent in the calculations and the standards. Anyone presented with the results of such calculations should take care to determine which vibration propagation equation was employed for the calculation and the suitability of the parameters used in it. These factors entirely determine the result, its meaning, and its applicability in a given situation and locale.

Correct and judicious use of appropriate ground vibration standards, combined with careful and scientifically valid vibration monitoring, can provide a sense of reassurance regarding vibration damage potential. Such an approach is not a "guarantee" of vibration safety, but it is far better than just guessing or hoping that damage will not be done. It is overwhelmingly more desirable than dealing with actual damage after it has occurred. Of course, there is simply no substitute for actual vibration monitoring done on the job itself.

A Note on Historic, Culturally-Important or Damaged Structures

The OSM velocity limit for blasting and the much lower construction-based FTA Class III limit for timber-framed homes, shown in the diagrams above, are not applicable for historic structures or those which have already suffered vibration damage. Typically, among the highest velocity (PPV) limits recommended in the scientific literature for such structures is the FTA Class IV limit of 0.12 in/sec (cf. FTA Class III limit of 0.2 in/sec shown in the diagrams above). A limit of 0.08 in/sec has been advised for the thousand-year-old masonry structure, Pueblo Bonito (seen at right), in Chaco Culture National Historical Park in New Mexico, USA.^[13] Vibration velocity limits as low as 0.05 in/sec appear in the literature for other historic structures.^[14] These lower limits have the effect of increasing safe distances, calculated using diagrams like the ones in this chapter, for historic or damaged structures (see Vibration and Damage and Vibration Safety in the CVDG Pro for examples illustrating this point).

Other Ways of Calculating Vibration Velocities

There are other, more complicated, less phenomenological, equations which can be used to calculate predicted vibration velocities at specific distances in construction and blasting environments. Some are simple adaptations of the FTA equation, whose modifications better account for those types of equipment which have variable source energies (e.g. pile drivers, vibratory compactors and pavement breakers).^[6],[38] A few variations in vibration calculation approaches are discussed in more detail in the CVDG Pro chapter, Calculating Vibration Amplitudes.^[9] However, none of them, no matter how many physical parameters are included, can take into account all location-specific variables like vibration wave interference, wave refraction and wave reflection from nearby building foundations, underlying rock layers, buried obstructions, and landscaping effects. Nor do they directly account for resonant amplification-related damage potential in homes, especially where vibration duration becomes a factor, as in construction.^[10]

The more advanced forms of vibration velocity calculation are valuable scientifically and theoretically. Their importance should not be underestimated. However, they do not guarantee greater accuracy in calculation of velocities in a specific situation and at a specific structure than do simpler calculation methods.

Applicability of Vibration Calculations

Calculations of vibration PPV's assume a greater importance than their usual accuracy might warrant, because vibration monitoring is so rarely done on construction jobs, even when required by contract or regulation. Even when it is done, the monitoring data may not be acknowledged or made available by contractors. I have not tried to present here a complete analysis of all the ways of calculating how vibration velocities vary with distance, as such an analysis is probably well beyond the needs or interest of most people. However, it is fair to say that all the calculation approaches that have been developed to date have limitations in scope, accuracy and applicability. They also usually suffer from a lack of applicable data at a given site for best implementation of them. Both comparison of calculated velocities with measured data and the limitations of the equations themselves suggest that even the more physically-realistic equations can be considered only as ways of approximating actual ground vibration velocities and the related "safe distances". Even when local soil conditions are explicitly measured and taken into account, these more advanced approaches to vibration velocity/distance relationships can be in error with respect to measured vibrations by a factor of two or more.^[5]

This is the reason that we have recommended throughout the CVDG (e.g. Vibration Regulation) that, when calculations are used to estimate vibration velocities, they be subjected to careful validation in the locale of interest and at least a two-fold safety factor be built into any velocity standard or "safe distance" derived from them.^[31] Any vibration-causing operation with a calculated PPV near the upper limit of that two-fold safety factor calls for implementation of mitigation measures. Vibration velocity calculations can be very valuable in understanding how far from the vibration source damage might occur and under what conditions. But, that value is greatly increased when the equations are employed with real understanding of how they can be scientifically applied in the local vibration environment and what their limitations might be.^[34]

E-mail to drzeigler@vibrationdamage.com or send online questions or comments about Vibrationdamage.com.
https://www.vibrationdamage.com,  ©Copyright 2013-2024 John M. Zeigler
Last modified: 02/29/24